To check whether any four given points construct a proper quadrilateral on the Cartesian plane, click the following button. If it is a special type of quadrilateral (like rectangle, square, rhombus etc), I will mention that. Also, the lengths of the sides and the diagonals along with the area will be determined.

Here 'proper quadrilateral' means convex quadrilateral. Chances are, all the quadrilaterals that you have encountered till date are convex quadrilaterals. Each internal angle of such a quadrilateral has a magnitude of less than 180^o. The following is an example of a convex quadrilateral.

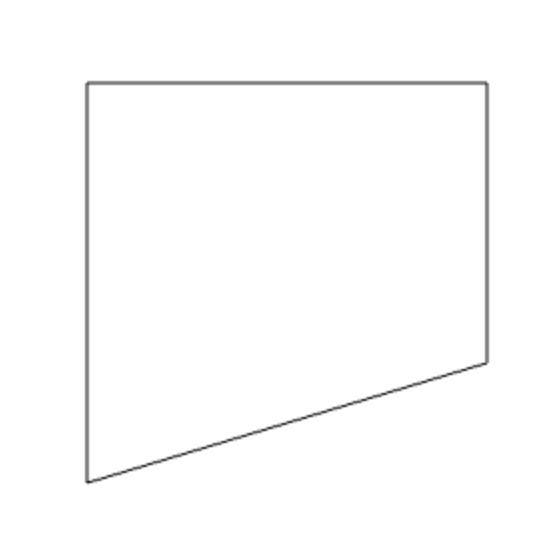
So there might be a question as to, what does a concave quadrilateral look like? It does as follows:

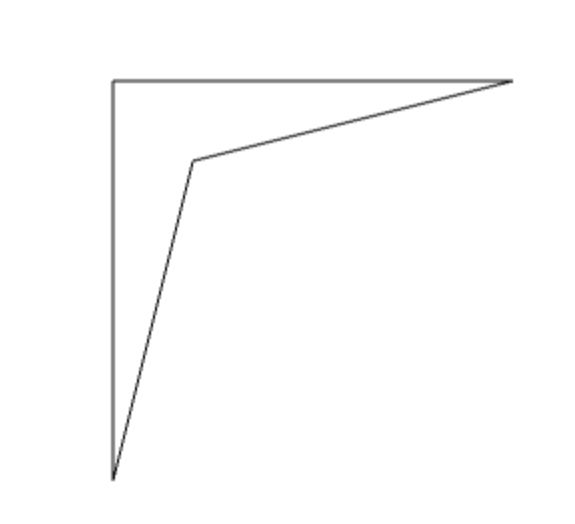
As you can see, one interior angle of a concave quadrilateral has a magnitude of greater than 180^o. A set of four points which forms such a quadrilateral, in whatever order the points may be taken, will always form a concave quadrilateral. These points will never form a convex or 'proper' quadrilateral. An example of a set of four such points are: (0,0),(10,0),(3,3),(0,10).

On the other hand, an example of four points that can be connected successively to form a 'regular' or convex quadrilateral are (0,0),(10,0),(8,8),(0,10). Let us name the points as A, B, C, D respectively. In this order the points will form a convex quadrilateral. However, if taken in a wrong order, such as A, C, B, D, the following figure will be obtained. This is clearly not a quadrilateral, but only two connected triangles with a common vertex.

Suppose, in an exam the question paper has a question on coordinates and quadrilaterals, where the points are listed in the wrong order. In that case, it is the responsibility of a student to find the correct order. In SSC 2024, there was such a problem in the higher maths exam of one of the boards. Each examiner then had instructions from the board that any candidate who 'touched' to answer the question would get full marks.

This should not be the case, as it is the students responsibility to find out in which order the points are to be taken to form a proper quadrilateral. This is actually part of the solution to the problem.

Also, if three or all of the given four points are collinear, then NO quadrilateral can be obtained. If three points lie on the same straight line, we get a triangle instead of a quadrilateral.

In order to return to the homepage, click the following link.